题目链接
这次不咕了
https://www.luogu.org/problemnew/show/AT2389
闲扯
考场20分爆搜走人 \cy
话说这几天T3都很考验思维啊
分析
我们先钦定一只鸡(虽然考试时是苹果但是我觉得杀鸡更亲切(因为我们某位同学))先必须活着,所以呢我们需要逆着倒推每一组关系,然后把为了保证我们钦定的鸡活着必须杀的鸡放进一个集合,为了方便表示用$f[now][i]=1/0$表示钦定第now只鸡活着第$i$只鸡最终有没有加入集合;
对于一对关系$(a,b)$,如果$f[now][a]=1$,那么$f[now][b]$显然必须置为1加入集合,因为a这只鸡为了保证now不被杀掉已经在一条边中被杀掉,为了保证当前这条边合法则必须杀掉b(注意关系是倒着枚举的)
但这是有个问题,就是如果$f[now][a]$&$f[now][b]=1$说明关系矛盾,$now$必须死,为啥?
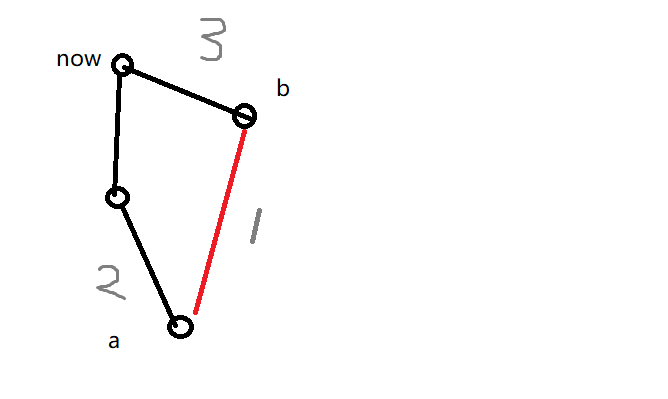
我们考虑没有这种情况,将鸡视为点,关系视为边,显然我们的集合实际上是一个以now为根节点的树,而且满足$x$到$fa[x]$的关系比$fa[x]$到$fa[fa[x]]$的边次序要早(但是在枚举时因为是倒着枚举是先构成前者)
如果这时候加入一条边连接两个已经在集合中的点$(a,b)$,由于1号边次序要比2,3边早,所以先必须在a,b中选一个杀死满足1号边的关系.但是我们为了让now不死,我们必须要让a点因为2号边死去,b因为3号边死去.出现了这种情况显然就不可能了,所以需要记录一下$now$存活是不可行的
最后假设已经遍历完,获得钦定每个点活着的时候要杀掉的鸡的集合(虽然不一定合法)
然后对于每一只鸡判断是否能与编号靠后的另一只鸡一起存活,怎么判断呢?
首先如果如果其中有只鸡本身无法存活则特判continue,但是还有种非法的情况,就是存在一只鸡为了满足$a$活必须死,又同时满足$b$活下来也必须死.这样的话$a,b$无法同时存活
这其实很显然的,边有先后顺序,你为了满足其中一只鸡另一只鸡就一定不可行,所以这种情况我们可以把两个鸡的集合并起来看看有没有1存在
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cctype>
#include <iostream>
#include <bitset>
#define ll long long
#define ri register int
using std::min;
using std::bitset;
using std::max;
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while(!isdigit(c=getchar()))ne=c=='-';
x=c-48;
while(isdigit(c=getchar()))x=(x<<3)+(x<<1)+c-48;
x=ne?-x:x;return ;
}
const int maxn=405;
const int inf=0x7fffffff;
bitset <maxn> o[maxn];
bool ok[maxn];
int a[100005],b[100005],m,n;
int main(){
int x,y;
bool flag=0;
read(n),read(m);
for(ri i=1;i<=m;i++)read(a[i]),read(b[i]);
for(ri i=1;i<=n;i++){
o[i][i]=1;flag=0;
for(ri j=m;j>=1&&!flag;j--){
x=o[i][a[j]],y=o[i][b[j]];
if(x&y){
ok[i]=1;
flag=1;continue;
}
if(x){o[i][b[j]]=1;}
if(y){o[i][a[j]]=1;}
}
}
ll ans=0;
for(ri i=1;i<=n;i++){
if(ok[i])continue;
for(ri j=i+1;j<=n;j++){
if(ok[j])continue;
if(!((o[i]&o[j]).any()))ans++;
}
}
printf("%lld\n",ans);
return 0;
}
|
