题目链接:
咕咕
闲扯:
哈哈这道T3考场上又敲了5个namespace,300+行,有了前车之鉴还对拍过,本以为子任务分稳了
结果只有30分哈哈,明明用极限数据对拍过不知怎么回事最后数据又是读不全,玄学,要是NOIP这样就GG了
首先第一个子任务贪心模拟即可,但是第二个子任务就像NOID1T1,你啥也不能输出但是我输出了0哈哈,真的是傻到家了,第三个子任务简单考虑一下即可;第四个子任务已经想到了偏正解的做法,但是用了个很SB的方法维护,昨天的T3也是这样但是都GG了…感觉退役钦定了
感谢WYT大佬正解讲解,高一神仙tql
分析:
先考虑第四个子任务,我说一下我在考场上的做法,我们设$pos[i]$是第i个任务的坐标,同时先将区间长度排序离线处理
先考虑pos[1]>0的情况,我们把相邻正负两点看成一对处理,所以我们可以一开始在负的点值那里加一个0点这样就凑成对了,考虑从一个负点右移到一个正点的时候,如果都不会出现不用右移的情况(也就是不会有直接覆盖正点的情况)答案就是上一次的总长度减去点个数乘以区间长度之差
但是如果出现了这种情况呢?首先我们离线处理是已经将区间长度从小到大排序,所以当前区间长度是这种情况下一个区间的长度肯定还会是这种情况。
所以遇到这种情况我们需要减去计算之前区间长度在这两点之间需要的移动距离,再将这两个踢出我们的考虑范围(我比较傻用了两个堆存储一个正点一个负点,由于是正值或负值是分别单调的只需要两个指针即可完成操作),同时点数减去2(成对考虑),再次计算贡献即可
pos[1]<0再分类讨论一下就好了
这种情况经过了对拍的检验应该是没什么问题的但是数据没读全也不知道咋回事
然后正解是怎么处理这个子任务的呢?我们可以把任务编号看成x轴,坐标位置看成y轴点出所有的点再将相邻两点连线是这个样子:
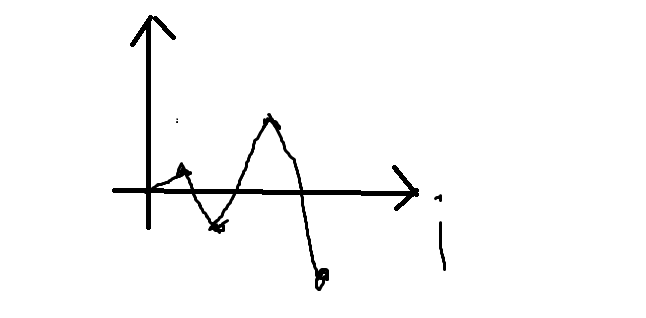
我们将相邻两点之间连线的长度叫做$p[i]$,当前区间长度为$L$,如果任意$p[i]>L$那么答案就是$\sum (p[i]-L)$
但是如果存在$p[i]<=L$呢,若$a,b$连线长度$p<=L$,那么我们将这两点删去,将$a-1,b+1$之间连新的线
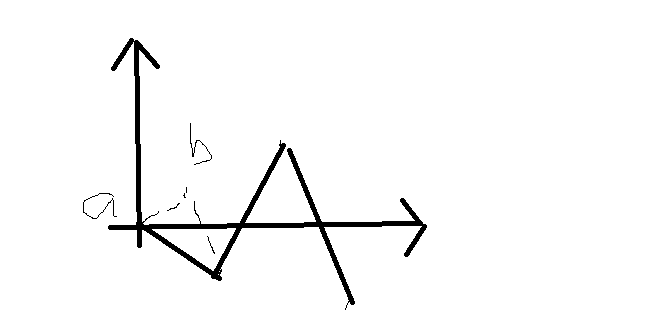
你会发现由于连线长度是单调的非常好处理,实际上我的做法也是在模拟类似的操作
再考虑没有第四个子任务的限制怎么做.首先我们可以预处理,对于一段连续的任务如果是单调的,那么我们只用保留头和尾就可以了,中间的显然不用管,那么这时候再仿照上面画出图像
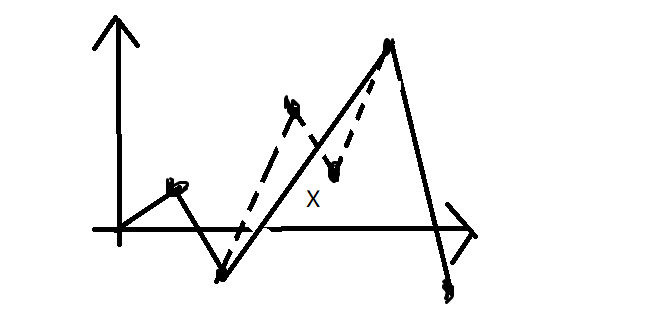
会发现由于并没有任务4的限制预处理后还可能出现x这样的点,这时候连线长度就不是递增的了,怎么办呢?
我们把所有长度放入一个小根堆中,每次对于一个新区间长度L,如果堆顶长度p小于等于L,也就是说达到x-1时就已经覆盖了x,比如图中$x-1$到$x$这段折线,我们就把它相邻两段连线包括它本身换成另一条折线,这样显然是最优情况
所以我们还需要记录连线的前驱后继来个映射,还要用链表/map记录下对应位移序列之类的搞一搞,统计方案用上面一样的方法,不断更新连线段数和连线总长就好了
由于每段只会进堆一次,时间复杂度$O(NlogN)$
但是这道题细节巨坑…题解只说了在首尾要特判,但其实链表之类搞一搞真挺烦的,所以并没有写代码…
代码:
这是标程代码…我太懒了并没有自己写一份
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
int n,m;
ll tot,ans[maxn];
vector<int> x;
vector<pair<int,int> > a;
map<int,int> mp;
inline ll calc(ll k){
if(!mp.empty()&&mp.begin()->second<0)
return tot-(mp.size()-1)*k;
else
return tot-mp.size()*k;
}
inline void solve(){
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
int t=0;
for(int i=0;i<x.size();++i){
tot+=abs(x[i]);
mp[i]=x[i];
q.push(make_pair(abs(x[i]),i));
}
while(!q.empty()){
int id=q.top().second,tmp=q.top().first;q.pop();
map<int,int>::iterator p=mp.lower_bound(id);
if(p==mp.end()||p->first!=id||abs(p->second)!=tmp)
continue;
while(t<a.size()&&abs(p->second)>a[t].first)
ans[a[t].second]=calc(a[t].first),++t;
if(p!=mp.begin())
if(p!=prev(mp.end())){
tmp=p->second,tot-=abs(p->second);
tmp+=prev(p)->second,tot-=abs(prev(p)->second);
tmp+=next(p)->second,tot-=abs(next(p)->second);
mp.erase(prev(p));
mp.erase(next(p));
p->second=tmp,tot+=abs(tmp);
q.push(make_pair(abs(tmp),id));
}
else{
tot-=abs(p->second);
mp.erase(p);
}
else if(p->second>0)
if(p!=prev(mp.end())){
tmp=p->second,tot-=abs(p->second);
tmp+=next(p)->second,tot-=abs(next(p)->second);
mp.erase(next(p));
if(tmp){
p->second=tmp,tot+=abs(tmp);
q.push(make_pair(abs(tmp),id));
}
else
mp.erase(p);
}
else{
tot-=abs(p->second);
mp.erase(p);
}
}
while(t<a.size())
ans[a[t].second]=calc(a[t].first),++t;
}
int main(){
freopen("z.in","r",stdin);
freopen("z.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=0,p,last=0;i<n;++i){
scanf("%d",&p);
if(p==last)
continue;
if(!x.empty()&&(x.back()<0&&p<last||x.back()>0&&p>last))
x.back()+=p-last;
else
x.push_back(p-last);
last=p;
}
for(int i=0,l;i<m;++i){
scanf("%d",&l);
a.push_back(make_pair(l,i));
}
sort(a.begin(),a.end());
solve();
for(int i=0;i<m;++i)
printf("%lld\n",ans[i]);
return 0;
}
|


