前言
在OI学习过程中,我们常常会发现一些题目(尤其数据结构题)中,一些数据的范围很大,但是涉及的数值的个数却很少,同时我们想用一个数组的下标与这些数据建立一一对应关系,这时我们就需要离散化
大致思路
对于一个大小为$N$不含重复数字的数组$a[N] (a[i]<=10^9)$,我们可以将$a[]$中的N个整数与$1$ ~ $N$这$N$构成一一映射关系,也就是说把$a[i]$用一个$1$~$N$中的数字代替,这样空间和时间复杂度都能变成与$N$相关
当然如果数组中有重复数据,你需要先去重(使用$std::unique$等)再进行上述操作
方式
结构体+$sort$
对于大小为$N$不含重复数据的整型数组$a[N]$,定义结构体
1
2
3
4struct Data{
int x;//原数组中的数据
int id;//原数组中储存x的下标
}d[N];然后以$x$为关键字进行排序,进行以下操作
1
2
3
4sort(d+1,d+1+N);//假设从1开始
for(int i=1;i<=n;i++){
a[d[i].id]=i;//按大小顺序离散化
}时间复杂度$O(NlogN)$ 空间复杂度$O(N)$
但是,使用这种方式的前提是数组无重复数据
$sort$+$lower $_$bound$
这应该是最常见的离散化方式
您只需要知道对于大小为$N$的数组$a[]$,
$lower $_$bound(a+1,a+1+N,X)-a$返回$a$中第一个大于等于X的位置
$unique(a+1,a+1+n)-(a+1)$返回将$a$数组去重后$a$的数组大小
然后就不难理解下面代码
1
2
3
4
5
6
7
8
9for(int i=1;i<=N;i++){
scanf("%d",&a[i]);
f[i]=a[i];
}
sort(f+1,f+1+N);
int nn=unique(f+1,f+1+N)-(f+1);//去重
for(int i=1;i<=N;i++){
a[i]=lower_bound(f+1,f+1+nn,a[i])-f;
}这样$f[i]$储存了从小到大排序后原来$a$中所有元素,$a[i]$中就储存了按大小排序后,原本$a[i]$大小的排名,$f[ \ a[i] \ ]$则返回原本$a[i]$的值
$map\&unordered $_$map$
如果您不知道STL中的$map$,建议您先去了解再来看此篇文章
其实思路很$naive$,知道$map$用法的应该都能看懂
1
2
3
4
5
6
7
8
9
10map <int,int> g;
int a[N],f[N],tot=0;
for(int i=1;i<=N;i++){
scanf("%d",&a[i]);
if(!g[a[i]]){
g[a[i]]=++tot;
f[tot]=a[i];
}
a[i]=g[a[i]];
}$f[a[i]]$就是原数组$a[i]$的值
但是$map$是用红黑树实现的,储存的元素是有序的
而$unordered $_$map$是用哈希表实现的
而在这里$map$纯粹只是起到了$hash$的查找与赋值,用$unordered$_$map$也能实现,相比较之下一般会更$unordered$_$map$快一点(实际上您可以手写一个哈希表完成上面的离散化操作)
然而使用$unordered$_$map$时注意,$C++11$之前使用需要
1
2
3
4#include <tr1/unordered_map>
using namespace std;
using namespace std::tr1;
unordered_map <int,int>g;$C++ 11$之后则可以使用
1
2
3#include <unordered_map>
using namespace std;
unordered_map<int,int>g;$pb$_$ds$中的$hash$_$table$
$pb$_$ds$中有许多黑科技,您可以在这篇博客中了解:
https://blog.csdn.net/Only_AiR/article/details/51940500
其中就有个$hash$_$table$,顾名思义,就是个蛤希表了,可以只用$find()$和$operator[]$,十分方便
然而使用它需要记一点东西,但你问我资不资瓷,当然是资瓷啊
1
2
3
4
5#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
cc_hash_table <int,int>g1;//两种hash_table,都跑得和香港记者一样快
gp_hash_table <int,int>g2;
后记
话说写这篇博客还是因为这道题
https://www.lydsy.com/JudgeOnline/problem.php?id=4241
我调整各种离散化方式来看看哪个最快,同时在luogu的个人私题中同步测试
然后给大家看看时间比较(因为怕影响大家评测把时间限制开的很小,难免会TLE,$bzoj$时限是80s)
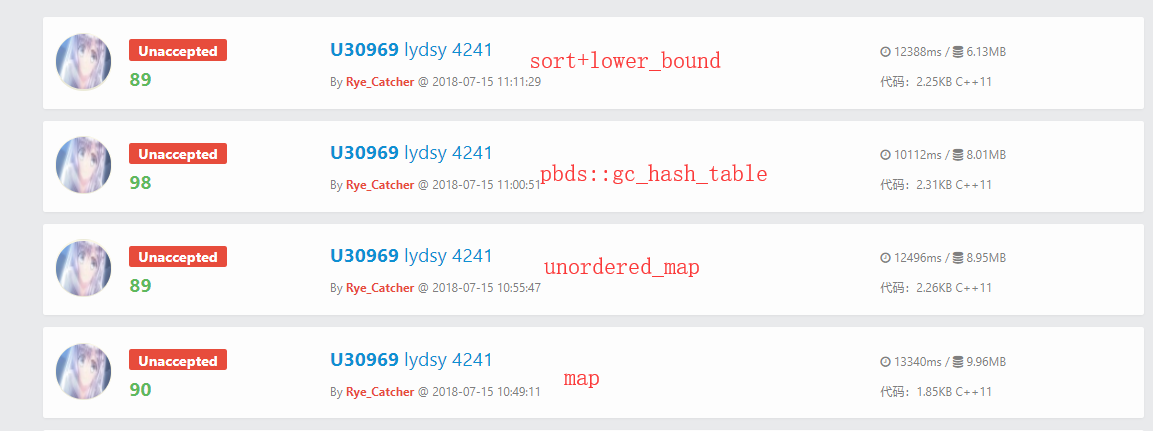
$hash $_$table$不知道高到哪里去
然而戏剧性的是BZOJ 上我测出来是$map$最快!!! $18000+ms$
其余的都比裸$map$慢了近$1000$~$2000+$ $ \ $ $ms$
很奇怪,BZOJ评测鸭太玄学了,如果有谁知道原因的可以解释下谢谢