学习笔记--Tarjan算法之割点与桥

前言

图论中联通性相关问题往往会牵扯到无向图的割点与桥或是下一篇博客会讲的强连通分量,强有力的$Tarjan$算法能在$O(n)$的时间找到割点与桥

定义

若您是第一次了解$Tarjan$算法，建议您反复阅读定义,借助图像来理解

  • 桥与割边

    对于无向连通图中点集的一个节点$x$,删去节点$x$及其关联的边之后,存在一对不联通的点对$(a,b)$,则称$x$是这个无向图的割点

    对于无向联通图中边集的一条边$e$,删去边$e$之后,存在一对不联通的点对$(a,b)$,则称$x$是这个无向图的桥或割边

    对于一般无向图,割点和桥可以指各个联通块的割点和桥

  • 时间戳:

    在对图的$DFS$中,按照节点第一次被访问的顺序,给各个节点标记一个值,该值称为时间戳,我们用$dfn[x]$表示$x$的时间戳

  • 搜索树

    在对图的$DFS$中,由于每个点只会被搜一次,所以访问经过的边构成了一棵树,称为搜索树,各个节点为根的子树称为$subtree(x)$,注意,$x \in subtree(x)$

  • 追溯值

    这个可以说是$Tarjan$算法的精髓了,在我个人看来,节点$x$的追溯值是指不经搜索树所能到达的所有节点中其时间戳的最小值或者它自身的时间戳.

    这看起来很难得到各个节点的追溯值,实则不然,分析一下,节点$x$的追溯值可以在一遍$DFS$中求得,请看下文介绍

算法

  • 性质一: 桥边都是搜索树上的边

    反证法,若桥边不是搜索树上的边,断掉这条之后仍可通过搜索树上的边保持图的联通

  • 割边判定法则

    无向边$(x,y)$是桥的充要条件是$dfn[x]<low[y]$(假设$y \in subtree(x)$)

    让我们想想为什么

    $low[y]$表示不经搜索树上的边$y$所能到达的所有节点中其时间戳的最小值,若$dfn[x]<low[y]$,根据定义和性质一,说明只有这条在s搜索树上的边$(x,y)$ ，$y$才能到达$x$,故边$(x,y)$是桥(割边)

  • 割点判定法则

    非根点$x$是割点的充要条件是存在一点$y (y \in subtree(x))$,满足$dfn[x]<=low[y]$,类比于上一法则,这里不再赘述

    当$x$为根节点时至少要有两个点满足上述条件

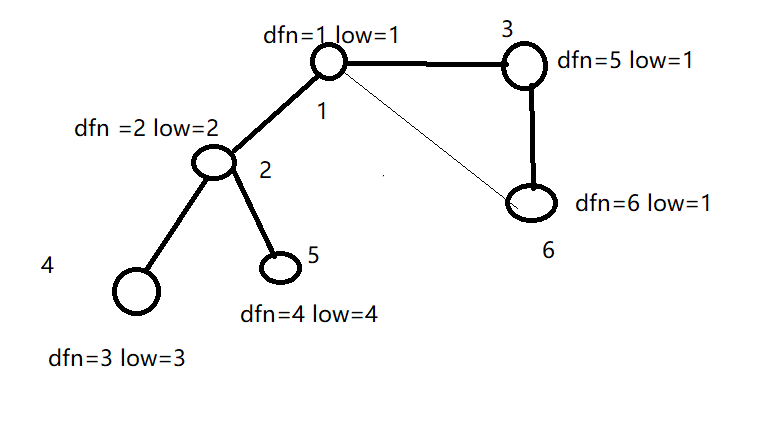
  • 大家可以通过图片理解上述过程,粗边都是搜索树上的边

    PM9Utx.png

注意

  1. 更新$low[x]$

    根据定义,我们只能用$x$在搜索树上儿子的$low[]$值或是一条非搜索树边$(x,y)$中的$dfn[y]$来更新$low[x]$

  2. 重边

    在求桥时,若节点$x$与其父亲间有重边,则其中只有一条算搜索树上的边,其他都是非搜索树上的边,可以用来更新.

    然而求割点时,由于是点与点联通关系不必考虑重边

代码

  • 桥

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    int dfn[maxn],low[maxn],cnt=0;
    bool bridge[maxm];
    void tarjan(int u,int in_edge){//in_edge--边的编号
    int v;dfn[u]=low[u]=++cnt;
    for(ri i=h[u];i;i=edge[i].ne){
         v=edge[i].to;
         if(!dfn[v]){
             tarjan(v,i);
             low[u]=min(low[u],low[v]);
             if(low[v]>dfn[u]){
                 bridge[i]=bridge[i^1]=1;
             }
         }
         else if(i!=(in_edge^1)){ 
         //in_edge^1表示反向边,不是反向边说明是非搜索树边
                 low[u]=min(low[u],dfn[v]);//通过非树边更新
         }
    }
    return ;
    }

  • 割点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    int dfn[maxn],low[maxn],root,tot=0;
    bool ans[maxn];
    void tarjan(int now){
    int v,flag=0;dfn[now]=low[now]=++tot;
    for(ri i=h[now];i;i=edge[i].ne){
        v=edge[i].to;
        if(!dfn[v]){
           tarjan(v);
           low[now]=min(low[now],low[v]);
           if(dfn[now]<=low[v]){
               flag++;
               if(now!=root||flag>1)//根节点要有两个满足条件
               {
                    if(!ans[now])ans[now]=1;//是割点
               }
           }
        }
        else low[now]=min(low[now],dfn[v]);
    }
    return ;
    }

例题